Countries handle private education in vastly different ways. Some countries have a lot of it. Some have none of it. The US has fewer students in private schools than most other countries, but as a result compared to other countries our private school students are quite wealthy.
Here is a graph showing the percentage of students in different countries attending private school. The red parts are truly private; the grey parts are dependent on government funding but privately operated, so sort of like charters in the US:
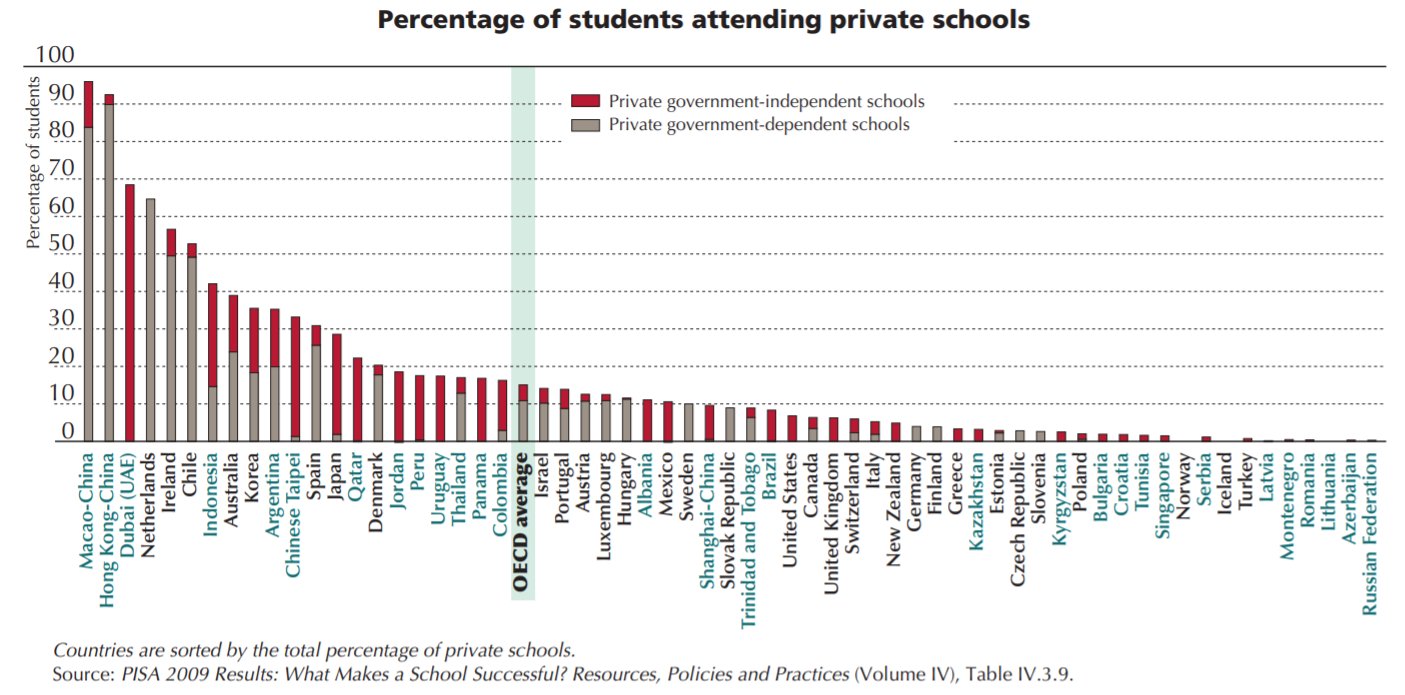
In the US, there is a fancy private school to fancy college pipeline. Fancy colleges are a font of inequality. Which leads many to a tempting thought: what if we banned private schools? What if we simply passed a law that made it illegal for such schools to exist on the grounds of promoting education equity, as many people have suggested?
Let’s take a closer look at banning private schools.
THAT IS DEFINITELY ILLEGAL
The first thing that would happen is that courts would declare the law unconstitutional. We know this would happen, because it already happened. In 1922 the state of Oregon passed the Oregon Compulsory Education Act. The law’s main target was Catholic schools, but it impacted all private academies. The law made it so that one could not fulfill their compulsory education requirement through private school attendance. Unless you had some other exemption (e.g. homeschooling) you had to attend your local public school.
The Ku Klux Klan were really pushing this law in Oregon. At the time they were huge defenders of public education, and this was all part of a national panic about immigration. (The Immigration Act of 1924 was a few years away.) Cited in David Tyack’s piece, here is the statement put forth by the Oregon Klan’s Grand Dragon: “The Klan favors … The American public school, non-partisan, non-sectarian, efficient, democratic, for all the children of all the people, equal educational opportunities for all.”

Anyway, the state was sued and the case made it to the Supreme Court. The Supreme Court was, like, nah man, this is very unconstitutional. It violates the 14th Amendment, the one that extends the rights of liberty to all citizens:
The fundamental theory of liberty upon which all governments in this Union repose excludes any general power of the state to standardize its children by forcing them to accept instruction from public teachers only. The child is not the mere creature of the state; those who nurture him and direct his destiny have the right, coupled with the high duty, to recognize and prepare him for additional obligations.
The world of 2021 is of course very different from 1922. The people in favor of banning private schools today are absolutely not trying to Americanize immigrants. They are definitely not the KKK. Still, it’s very illegal in this country to ban private schools.
WE DID IT ANYWAY
Oh, I don’t know how. We change the constitution. The Supreme Court reconsiders. We find some weird loophole in the 14th Amendment, and also the 1st Amendment. Reboot the universe with a magic ring. Whatever.
As of 2017, about 10% of the nation’s students are in private schools, which makes 5.7 million students. That percentage has been declining slowly, with the loss mostly felt by Catholic schools. About a quarter of private school students attend nonsectarian schools. The rest attend religious schools.

What sort of religions are we talking about? Mostly Christian, mostly Catholic, followed by Jewish.

The United States of America is a bit of a global outlier when it comes to teaching religion. We are the land of strict separation of Church and State. But in much of Europe some sort of non-doctrinal religious education is compulsory. In Finland, a course in religious education is compulsory but you get to choose your flavor depending on your religious beliefs. According to a professional organization for Finnish religion teachers: “In 2012 91.9% of pupils in comprehensive school took part in Evangelical-Lutheran [Religious Education], 1.4% in Orthodox, 1.5% in Islam, 0.5% in other religions and 4% in secular Ethics.” Seems like most people just go with the flow and take the Lutheran course. Still, a nice gesture.
Here’s a soft prediction for this fantasy scenario: if private schools were ever banned in the United States, we would end up letting schools teach religion again.
Another soft prediction: We would have to get more serious about religious accomodations more generally. For example, in New York City providing kosher or halal food in public schools is still at the “let’s try this interesting experiment” stage and not “we give you the food you’ll eat” stage. But most Jewish students who keep kosher attend private schools. If you got rid of those schools, you’d need to decide how to deal with religious kids with restrictions.
ENOUGH ABOUT RELIGION, LET’S BAN PRIVATE SCHOOL FOR RICH PEOPLE
About 2.5% of US students are attending non-sectarian schools. I don’t know where this 2.5% falls on the wealth spectrum, but give-or-take special programs and financial aid, yeah, let’s go ahead and assume that these kids are all pretty well-off financially.
What happens if they all go into the public school system?
The first thing is that scores for these students, particularly math scores, would probably go up. Private schools as a sector underperform public schools on math tests, as argued in detail by “The Public School Advantage.”
At least in the US, I don’t think it’s particularly mysterious why scores would go up. The government surveys schools to see how much time they spend on various subjects. With the autonomy that private school purchases, these schools spend less time on math.
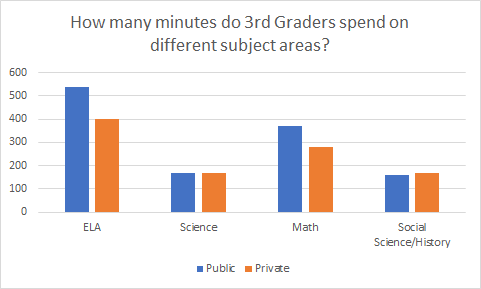
That’s a more or less minor point, but I think it’s helpful to remember that asking private school kids to return to public school has the potential to exacerbate certain inequalities, even as it reduces others.
But that’s small stuff. The big, lasting impact of eliminating private schools would be out of control residential segregation. Even more out of control than it currently is.
Julie Halpert wrote a really phenomenal piece about public and private schools that catalogs some of what you might expect in a pure public system. Wealthy people can — and frequently do — use their money to create insanely privileged institutions within the public school system:
On average, home prices near high-performing schools were $205,000 more expensive than they were in areas with low-performing ones. This suggests that in an all-public-school world, those with means would likely buy real estate in well-resourced districts—removing their resources from needier school communities and diluting from those poorer areas the pool of high achievers who experts say can benefit lower-performing students.
If you put wealthy students from powerful families back in the public school system, the main thing you’d get is more ultra-wealthy public schools. It’s hard to see how poorer students benefit from that.
And if that doesn’t work, wealthy parents who are sharing a district with poorer ones have another tool in their kit: they can secede, forming a newer, “higher performing” district:
Between 2000 and 2016, 63 communities split off from their existing school districts to form new ones. In just the last two years, 10 more communities have followed. Most of the new districts are more affluent, and less racially diverse, than those they left behind. Another 16 communities are actively exploring efforts to form their own school districts, according to the report.
But would this be widespread? Would there be some benefits for poorer students on the margins? Maybe policies and tests would be more reasonable if wealthy students were subjected to them?
I don’t know. Maybe. Though our system seems to accomodate plenty of double standards currently, so I don’t see why we couldn’t end up with music classes for rich public school kids and test prep for the poor, just as we have now.
To me, the problems in this country are the problems of wealth, and eliminating the most obvious manifestations of extreme wealth would do nothing to solve those problems. You’d just end up with slightly less apparent inequalities within the public school system. It’s like trying to reduce food inequality by banning high-end steakhouses. Or, for a much closer analogy, trying to improve health outcomes for poorer Americans by banning conscierge medicine. Ban private schools for the wealthy and we’ll just have a dozen more Thomas Jefferson High Schools.
In short: it’s definitely illegal to ban private schools for wealthy students. But even if you could all it would do is increase their math scores and more importantly spur the creation of new ultra-wealthy schools and school districts. This already happens in the public school system — the only reason it’s not worse at the moment is because so many wealthy students are educated privately. I don’t see how that leads to equity.
But maybe, if we really did pull off the ban, my kids would be able to get kosher food in public schools, which would at least be something.











