Not much is going very well in this most cursed school year, but I like the way I rewrote this lesson today.
Here is the original activity, from the Illustrative Mathematics Algebra 1 course:



I like the idea, but I saw room for improvement. Here were my issues:
- The problems were somewhat repetitive.
- Students could answer the questions without using the function expressions.
- This might make it so they’d miss the main ideas until the last two questions.
- I like creating situations where students have a principle that they try to apply to a lot of different situations. The way this is designed, they wouldn’t be applying any sort of general mathematical principle until the very last question.
For my redesign, I wanted to get a generalization out in front. I started by showing a parabola and asking students to identify the x-intercepts and the y-intercepts.

Then, I displayed a worked example showing how someone could use the standard form formula to find the y-intercept. I asked students to read all the text that was in green and to put their thumbs up when they were done reading. Then, knowing I had some deeper questions coming up, I explained each line of the example. “Because the y-intercept is always on the y-axis, we know that x will equal … say it aloud,” I gestured for everyone to chime in. “That’s right, x will equal 0. If you input that into the function, your output will be the y-coordinate of the y-intercept.”

After briefly explaining, I revealed those deeper questions:
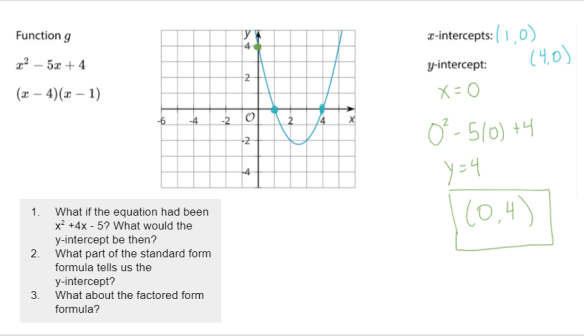
First, a “what if” question that swapped the numbers from the original function around. Instead of “-5x + 4” I asked about “+4x – 5.” What would the y-intercept be if the function looked like that? This question is asking students to take a step towards a generalization, and that second question goes all the way towards generalizing.
The third question, “What about the factored form formula?”, is a bit of an extension question. It was a more challenging question than I could have asked at this stage if I hadn’t lead off with the example. I didn’t expect every student would necessarily arrive at a correct answer to this question, but every student could benefit from trying to apply what they’d learned to factored form.
As it happened, there was a nice little debate about whether the y-intercept could be recovered from factored form. One student said, only if you turn factored form back into standard form by multiplying. Another chimed in to say that they noticed that -1 x -4 = 4, which connects to the y-intercept, but they weren’t sure if it were a coincidence. Then a third kid pointed out that -1 x -4 would always be part of the binomial expansion, so it wasn’t a coincidence. And then I pointed out that the same logic as before — input x = 0, your output is the rest of the y-intercept — applies to factored form, and (0 – 1)(0 – 4) = 4. Good talk.
Then, it was time to apply this knowledge. I started with a question that was probably a bit too easy, but I wanted a chance to connect factored form to the graph one more time. I asked students to put a thumb up when they’d found the x-intercepts of this function:

Good, good, I asked them to shout out the x-intercepts and I pointed out that they could have gotten this just from the equations. Ditto for the y-intercepts.
Anyway, on to the good stuff. I assigned partners and asked students to talk together about what the x- and y-intercepts were of this function:

Surprisingly challenging for the kids, even given all that we’d talked about! Most got the x-intercepts, the y-intercept required a bit more discussion. All were interested in the reveal, where I removed the grey box.
Moving along, I asked students to talk to their partners about the x- and y-intercepts of this graph:

And then this one:

This one threw kids for a loop! There was much discussion among pairs as to what the “other” x-intercept was going to be. And then there audible “ooohs” from a few kids when I revealed the graph, and there was only one x-intercept.
I feel as if it’s important to mention at this point that this was a class of pretty strong students. Their reaction to this graph says as much about them as it does about me. I want to be real, I don’t often elicit “ooohs” from my teaching. I don’t even know if I want to be a teacher that gets a lot of “ooohs.” But I want to tell you the truth, and the truth is that there were “ooohs.” I could be making that up, but I’m not.
Finally came the “Are you ready for more?” problem from Illustrative Math:

The lesson as written by Illustrative Math was pretty good, but it definitely fell into a paradigm that we might call “Notice, Notice, Generalize, Apply.” To give students enough mathematical data to make the generalization the lesson asks kids to do something a bit repetitive — to find a lot of x-intercepts and y-intercepts. Because students don’t yet know how to use formulas to do this, the graphs need to be provided. Because the graphs are provided, kids will probably just use them. Only at the end, when they’re prompted to generalize, will kids go back and try to connect their answers with the formulas. Kids then are asked to apply that generalization to a single new case where a graph wasn’t provided.
My rewrite follows a different paradigm, something I’ve sometimes called “Analyze, Explain, Apply,” but might also be called “Generalize, Apply, Apply, Apply.” The generalization is front-loaded in the lesson, which means that I was able to turn some of those “notice” problems into chances to apply the big idea about using the formulas to find the intercepts. I hope it’s clear that this hardly eliminated the challenge for students. If anything, it deepened our mathematical discourse.
The generalization is the thing we want to help students think about. Sometimes it can be nice to give students a chance to form that generalization on their own. But the tradeoff is that they then have less time to try out that new mathematical idea with new problems. If you put that big idea towards the top of the lesson, they get many more chances to apply the idea to problems. Of course, that means that you have to provide that new idea to students, either in the form of an example or an explanation. That’s a trade that I’m increasingly willing to make.