The basic theory is that people often learn things via a two-step process: they watch what someone else does and try to do it on their own. This isn’t the only way that people learn, but in its broad strokes covers a surprisingly large number of cases, at many different scales of learning. Parent shows baby how to play with ball, baby tries to bounce ball. New kid sees cool kids wear trendy shoes, learns to imitate their interests and affectations. Elizabethan poet-playwright writes awesome murder play, contemporary screenwriter writes mediocre murder movie.
Sure, but what about when this is very hard? If it was easy to imitate excellence, everyone would do it. It helps if you can impose some sort of structure on the effort. Sometimes it’s useful to focus on imitating just one step at a time. Other times you need to better understand what that other person did. Hopefully this is starting to sound familiar, it is typically called “teaching.”
Specifically in the context of math or science and learning procedures, there is a method for structuring this kind of learning called “fading a worked example.” I don’t remember where I first heard of it, but it’s strongly associated with Alexander Renkl’s research. Here’s how it works:
- Show someone a task and perform all of it for them.
- Then, present a new task, and perform almost all of it for them, everything but the last step. They do they last step on their own.
- Present another new task, and let them handle a bit more of it on their own. Ask them to do the last two steps.
- Etc., until the person is performing the entire task on their own.
Last week I did this sort of activity with my calculus class. It started with a fully worked example, that I prepared before class and asked students to analyze:

Then, I started knocking out steps from the procedure, starting at the end. This lets kids practice just that step, but in a meaningful context. (That is, the context of the integration problem.)
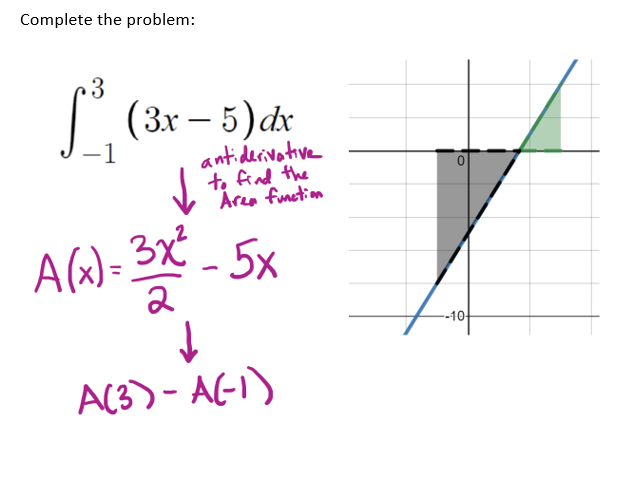
And then I knock out some more steps.
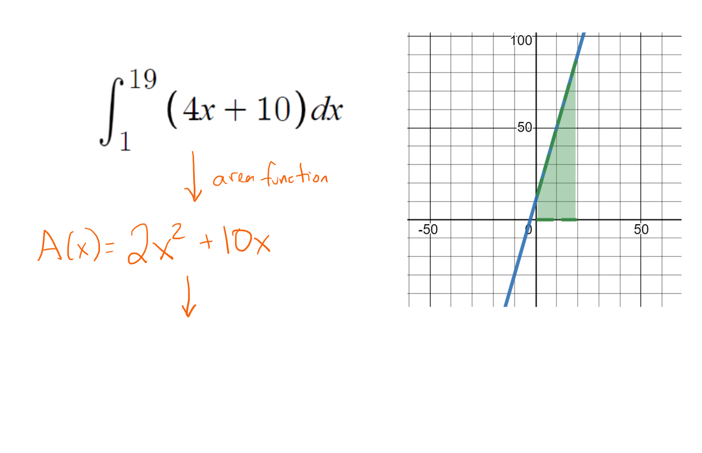
And by the end, they should be able to try the problem all on their own.
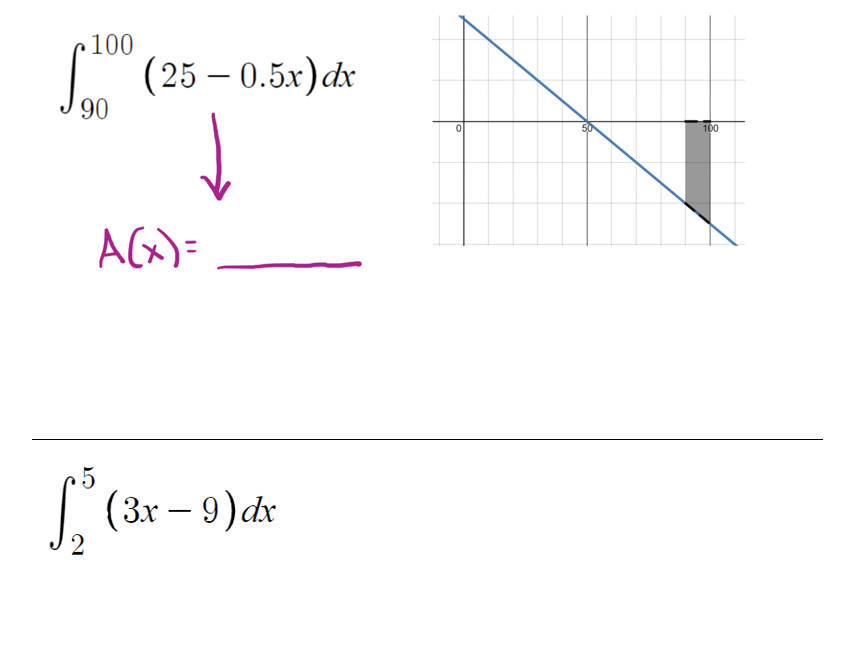
Here is another fading activity I ran in class last week, this time with my 8th Graders. I was teaching writing expressions for linear situations. At first I gave them the expression and asked them to think about why the expression fits the scenario:

But soon after I was leaving out the expression and asking them to provide it:

As I describe in my book Teaching Math With Examples, these sorts of tasks do much more for students than I first expected them to:
“As my class got to work, I was surprised by how challenging the assignment was. Students were asking me good questions about mechanical issues I hadn’t even considered to be problematic for them. It turns out that lurking beneath their overall struggles had been a variety of smaller difficulties. The faded-out exercise gave them a chance to systematically work on all of them.”
I find myself using these faded worked examples the day after a rough class. One where every student seemed to do great right up to the moment when I asked them to try the problem on their own. It’s for those days when the class seemed nervous about even starting, not because the problem was opaque but because the solution seemed like just SO MUCH.
It’s worth pointing out that this is not rocket science. Which makes sense, because teaching is not rocket science. It’s not science? It might be fair to say that teaching is maybe cognitive science plus other educational research plus a lot of random practical knowledge multiplied by a ton of emotional intelligence. The point is that you don’t need a researcher to invent something like fading a worked example.
One the other hand, I learned about this from reading research. And then, after I read about it in research, I sat on that knowledge for a few years. I wasn’t sure if it would fit in with the rest of my random practical knowledge about teaching. I also was worried that it would be dull and repetitive to my students, throwing off the mood in the room. (I shouldn’t have worried, it’s great.) Now that I’ve tried it a lot in my teaching, I’m happy to share the idea with enthusiasm.
Research is great, but that will only ever be a part of what it takes for a good idea to make its way into practice. The people who use the idea need to chew on it for a while and make sure it fits in with everything else. It would be good if researchers understood this, because it implies different sort of studies than what is frequently done. (“We Did This One-On-One With a Bunch of Undergrads Which Reveals Universal Teaching Techniques and Now Go Ahead and Use It.”)
Anyway, if you’ve got a long-ish procedure and it’s a topic that is easy to create many similar-ish examples for, you might consider writing a worked example and fading out the steps, starting at the finish.