Problem 1-14 from Challenging Problems in Geometry:


This took me a while to understand, but once I had a sketch it didn’t take me very long to use isosceles triangles to show that there were a bunch of congruent triangles in the diagram. I did this on paper, but thought it would be nice to put this into Geogebra.
The most satisfying diagram came when I started with a square, ala Challenge 1:
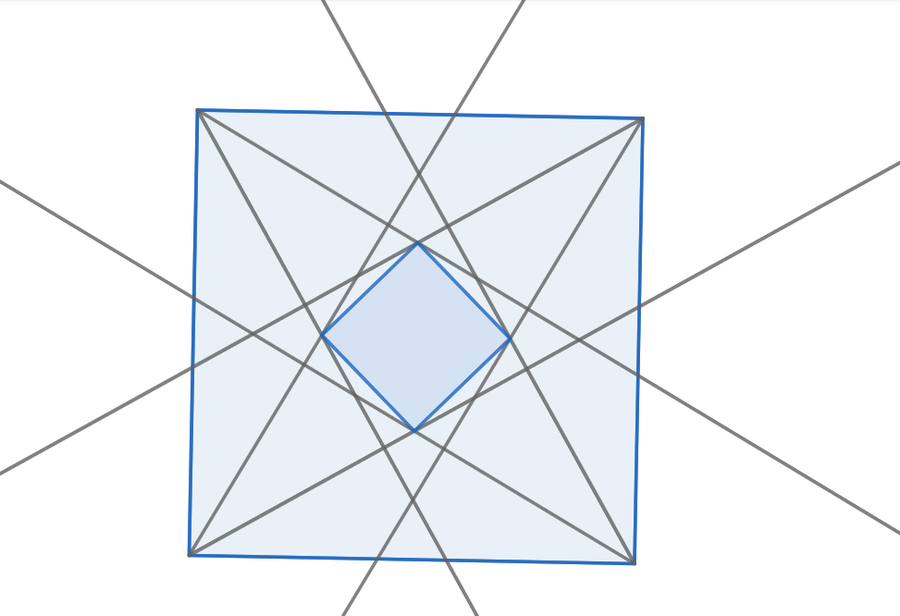
From attempting this problem and then studying the solution I didn’t feel as if I learned any new techniques. But this result is really awesome, and it’s one that I want to remember. It reminds me of midpoint quadrilaterals — the quadrilaterals formed by connecting the midpoints of a 4-gon. It’s pretty.
Ooh! Just looking at this now, it occurs to me that I should be asking “what is the ratio of areas between the original square and the trisector-square?”
I just tried to calculate it … I got , or about 8%. Seems to check out.
After the last few problems took a lot of energy, it was nice to feel this one come a bit easily.
***
The next problem wasn’t an immense struggle either, mostly because I didn’t have paper around so I just skipped to the hint.


Like I said, I didn’t have paper and I wasn’t sure what to do, so I skipped to the hint.
It’s a nice hint:

These theorems say:
- If a line is perpendicular to another line m, it’s also perpendicular to any lines m is parallel to.
- Side splitter: connect two midpoints of a triangle and you get a line parallel to the other base
I very much enjoyed taking those hints and figuring out how to use them, even though it didn’t take too long.

The result isn’t so interesting to me, but I think there is a problem-solving takeaway:
Takeaway(s): If a diagram has a lot of midpoints, there’s also a lot of parallel lines.
If you’re trying to prove that an angle is 90 degrees, try to start with all the other 90 degree angles in the diagram. See if they lead to other right angles.
***
I’ve been reading a lot about self-explanation lately. This is a notion emerging from cognitive science research that suggests an important part of learning is explaining things for yourself — making inferences beyond what is explicitly there. This is often seen as crucial for learning from worked examples, i.e. solutions. This is something I am doing as part of this geometry project.
In one of his papers (let me know if you want the reference) Renkl distinguishes between different types of self-explanation. One that he thinks is particularly relevant for learning math is principled explanations. In other words, connecting specific examples to general principles. It makes sense that this would be useful — it means you can use this specific example to help with other problems!
The thing that I’m realizing while studying geometry is that without a teacher’s help, I’m basically guessing as to what the general principles are. I think my “takeaways” above could be useful for tackling other problems, but I don’t really know for sure. This is relatively new to me! I won’t know for sure until I find a chance to use the techniques in another problem.
I guess this is just another way that learning from a teacher is easier than learning on one’s own.