
I’m falling in love with Classic Set Theory, an introductory set theory text. The introduction to Russell’s paradox motivates it in a way that I’d never seen before.
When I’ve thought about Russell’s paradox in the past I’ve sometimes thought, ok, this makes sense, but how did he come up with this? Or, even, what line of thought could even have led to conceiving of something so clever?
(Russell’s paradox is one of the great stories of math: a letter to Frege, just as he’s completing his master work, announcing a fatal contradiction in his system, effectively ending Frege’s life’s project. Wow! The above panel is from Logicomix, a book that I left feeling disappointed by. I felt it didn’t live up how awesome the story is, but maybe my expectations were just too high.)
Anyway, here’s what I think I currently understand:
Frege figured out a way to define “1” without talking about oneness. Instead, he made it all depend on uniqueness.
Definition: A set 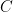 is a singleton if there is an
is a singleton if there is an  and if anything else is in
and if anything else is in 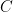 , that thing is equal to
, that thing is equal to  .
.
Frege doesn’t say anything about the number “1” in defining singletons; it all depends on equality. So Frege is free to use the notion of singleton-ness to define the number “1”.
Definition: There is a set of all the sets that are singletons. Call that set ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=000&s=0&c=20201002) .
.
It’s a pretty nifty trick, and it shows that lurking within our notion of equality is some notion of oneness.
So far, that’s Frege: “1” is a set, ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=000&s=0&c=20201002) .
.
But if ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=000&s=0&c=20201002) is a set, we can start playing around with that set. For example, can make a new set that contains just one element:
is a set, we can start playing around with that set. For example, can make a new set that contains just one element:
![\{ [1] \}](https://s0.wp.com/latex.php?latex=%5C%7B+%5B1%5D+%5C%7D&bg=ffffff&fg=000&s=0&c=20201002) is a singleton!
is a singleton!
Which leads to the weird notion that ![{ [1] }](https://s0.wp.com/latex.php?latex=%7B+%5B1%5D+%7D&bg=ffffff&fg=000&s=0&c=20201002) is a member of
is a member of ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=000&s=0&c=20201002) . And, of course,
. And, of course, ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=000&s=0&c=20201002) is in ${ [1] }$ itself, so we get a weird series of inclusions:
is in ${ [1] }$ itself, so we get a weird series of inclusions:
![[1] \in \{ [1] \} \in [1]](https://s0.wp.com/latex.php?latex=%5B1%5D+%5Cin+%5C%7B+%5B1%5D+%5C%7D+%5Cin+%5B1%5D&bg=ffffff&fg=000&s=0&c=20201002)
Not paradoxical yet, but weird. And close enough to Russell’s paradox that you can see where he might have started playing around with these ideas. OK, so there’s a weird way that ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=000&s=0&c=20201002) as defined by Frege is a member of itself. How could we mess around with that idea some more?
as defined by Frege is a member of itself. How could we mess around with that idea some more?
Definition: V is the set of all sets.
And then clearly, V is also a member of itself.
And now we’re so, so, so close to Russell’s paradox itself: the set of all sets that doesn’t include itself.
Part of what I find so exciting about all of this is the connection to Frege, but also the sense that there’s a natural progression from the definition of “1” to the paradox. What it is is that the definition of “1” does open the door to weird inclusions, since it’s a set of everything that is a singleton. And once that door is open, everything can march on through.
The only way to close that door is to restrict what is allowed to become a set.

